binder

sktime 中的基于划分的时间序列聚类#

基于划分的时间序列聚类算法是从 n 个时间序列中创建 k 个聚类的算法。聚类中的每个时间序列彼此同质（相似），与聚类外的异质（不同）。

为了衡量同质性并将时间序列放入聚类中，使用一种度量（通常是距离）。此度量用于将时间序列与代表每个聚类的 k 个其他时间序列进行比较。这些表示使用模型训练时的统计采样技术得出。然后，时间序列被分配到最相似（或基于度量得分最高）的聚类，并被称为该聚类的一部分。

目前，Sktime 中支持 2 种划分算法。它们是：K-means 和 K-medoids。下面将进行演示

导入#

[1]:

from sklearn.model_selection import train_test_split

from sktime.clustering.k_means import TimeSeriesKMeans
from sktime.clustering.k_medoids import TimeSeriesKMedoids
from sktime.clustering.utils.plotting._plot_partitions import plot_cluster_algorithm
from sktime.datasets import load_arrow_head

加载数据#

[2]:

X, y = load_arrow_head(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y)
print(X_train.shape, y_train.shape, X_test.shape, y_test.shape)

(158, 1) (158,) (53, 1) (53,)

K-划分算法#

K-划分算法是指那些试图创建 k 个聚类并使用距离度量将每个时间序列分配给聚类的算法。在 Sktime 中目前支持以下算法

  • K-means - 最著名的聚类算法之一。K-means 算法的目标是最小化称为惯性或簇内平方和的准则（使用簇内值的均值作为中心）。

  • K-medoids - 与 K-means 类似的算法，但它不使用每个聚类的均值来确定中心，而是使用中位数序列。在算法上，处理这些 k-划分算法的常用方法称为 Lloyds 算法。这是一个迭代过程，包括

  • 初始化

  • 分配

  • 更新中心

  • 重复分配和更新直到收敛

    • 中心初始化#

    中心初始化是第一步，并且已被证明对于获得良好结果至关重要。下面将概述三种主要的中心初始化方法

    • K-means、K-medoids 支持的中心初始化方法

      • Random（随机）- 在这种方法中，训练数据集中的每个样本被随机分配到一个聚类，然后根据这些随机分配运行中心更新，即对于 k-means，使用这些随机分配聚类的均值，对于 k-medoids，使用这些随机分配聚类的中位数作为初始中心。

      • Forgy - 在这种方法中，从训练数据集中随机选择 k 个样本

      • K-means++ - 在这种方法中，从训练数据集中随机选择第一个中心。然后计算训练数据集中所有其他时间序列与随机选择的中心之间的距离。接着从训练数据集中选择下一个中心，使得被选择的概率与距离成正比（即距离越大，时间序列被选择的可能性越大）。剩余的中心使用相同的方法生成。这意味着每个中心生成时，被选择的概率与其最近的中心成正比（即离已选择的中心越远，被选择的可能性越大）。

      </li>

    这三种聚类初始化算法已经实现，在构建 k-means 或 k-medoids 划分算法时可以选择使用，通过解析字符串值 'random' 表示随机初始化，'forgy' 表示 Forgy，'k-means++' 表示 k-means++。

    分配（距离度量）#

    时间序列如何分配给聚类是基于它与聚类中心的距离。这意味着对于某些 k-划分方法，可以使用不同的距离来获得不同的结果。这里不详细讨论每种距离，但支持以下距离，并定义了它们的参数值

    • K-means、K-medoids 支持的距离

      • 欧几里得距离 (Euclidean) - 参数字符串 ‘euclidean’

      • 动态时间规整 (DTW) - 参数字符串 ‘dtw’

      • 导数动态时间规整 (DDTW) - 参数字符串 ‘ddtw’

      • 加权动态时间规整 (WDTW) - 参数字符串 ‘wdtw’

      • 加权导数动态时间规整 (WDDTW) - 参数字符串 ‘wddtw’

      • 最长公共子序列 (LCSS) - 参数字符串 ‘lcss’

      • 编辑距离与罚项 (ERP) - 参数字符串 ‘erp’

      • 编辑距离限阈值 (EDR) - 参数字符串 ‘edr’

      • 移动度量 (MSM) - 参数字符串 ‘msm’

      </li>

    更新中心#

    中心更新是改进聚类质量的关键。如何进行取决于算法，但支持以下方法

    • K-means

      • 均值平均 (Mean average) - 这是一种标准的均值平均方法，创建一个新序列作为聚类内所有序列的平均值。在使用欧几里得距离时非常理想。通过将 'means' 作为 k-means 的 averaging_algorithm 参数来指定使用此方法。

      • DTW 重心平均 (DBA) - 这是一种专门的平均度量，旨在与 dtw 距离度量一起使用，因为它使用 dtw 矩阵路径来考虑对齐，从而确定平均序列。这为时间序列的均值提供了更好的表示。通过将 'dba' 作为 k-means 的 averaging_algorithm 参数来指定使用此方法。

      </li>
<li> K-medoids
    <ul>
        <li>Median - Standard meadian which is the series in the middle of
        all series in a cluster. Used by default by k-medoids</li>
    </ul>

    K-means#

    [3]:

    k_means = TimeSeriesKMeans(
    n_clusters=5,  # Number of desired centers
    init_algorithm="forgy",  # Center initialisation technique
    max_iter=10,  # Maximum number of iterations for refinement on training set
    metric="euclidean",  # Distance metric to use. Choose "dtw" for dynamic time warping
    averaging_method="mean",  # Averaging technique to use
    random_state=1,
)

k_means.fit(X_train)
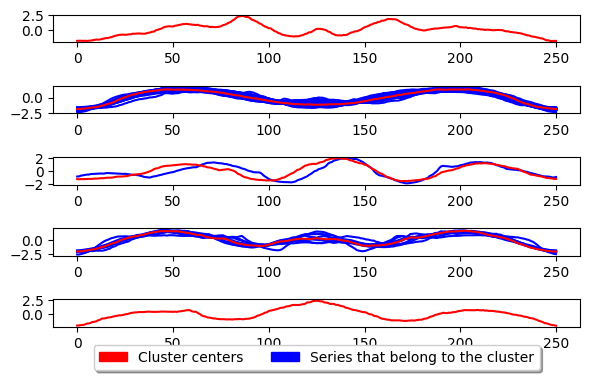
plot_cluster_algorithm(k_means, X_test, k_means.n_clusters)

    <Figure size 360x720 with 0 Axes>
    ../../_images/examples_clustering_partition_based_clustering_5_1.png

    K-medoids#

    [4]:

    k_medoids = TimeSeriesKMedoids(
    n_clusters=5,  # Number of desired centers
    init_algorithm="forgy",  # Center initialisation technique
    max_iter=10,  # Maximum number of iterations for refinement on training set
    verbose=False,  # Verbose
    metric="euclidean",  # Distance metric. Use "dtw" for dynamic time warping
    random_state=1,
)

k_medoids.fit(X_train)
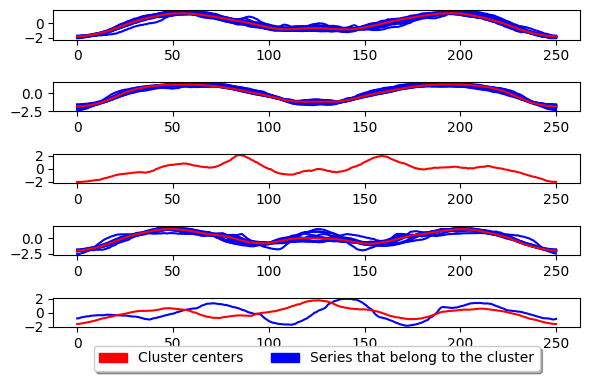
plot_cluster_algorithm(k_medoids, X_test, k_medoids.n_clusters)

    <Figure size 500x1000 with 0 Axes>
    ../../_images/examples_clustering_partition_based_clustering_7_1.png

    上面展示了 K-medoids 的基本用法。此算法的工作原理与 K-means 基本相同，但它不通过计算聚类内序列的均值来更新中心，而是选择中位数序列。这意味着中心是数据集中已存在的序列，而不是生成的。K-medoids 的关键参数是度量 (metric)，我们可以调整它来提高时间序列的性能。下面给出了使用 dtw 作为度量的示例。

    [5]:

    k_medoids = TimeSeriesKMedoids(
    n_clusters=5,  # Number of desired centers
    init_algorithm="forgy",  # Center initialisation technique
    max_iter=10,  # Maximum number of iterations for refinement on training set
    metric="euclidean",  # Distance metric. Use "dtw" for dynamic time warping
    random_state=1,
)

k_medoids.fit(X_train)
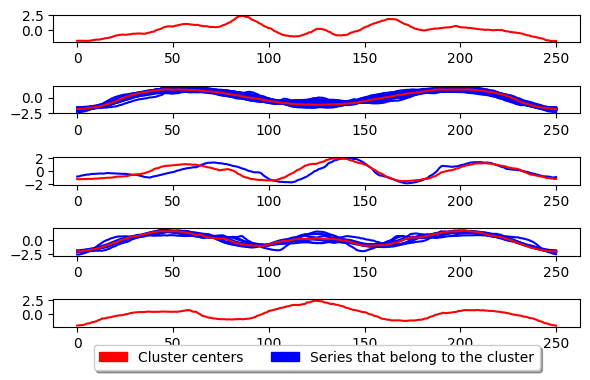
plot_cluster_algorithm(k_medoids, X_test, k_medoids.n_clusters)

    <Figure size 500x1000 with 0 Axes>
    ../../_images/examples_clustering_partition_based_clustering_9_1.png

    使用 nbsphinx 生成。Jupyter notebook 可以在此处找到。